Games and Puzzles

How would you like to toss some cards in the air?
Can you make triangles?
How about finding a path out of the maze that equals 100?

Addition Toss Up

Materials:

  • Deck of playing cards
  • paper
  • pencil

How to Play:

Shuffle the deck and place the deck face down.
Each player draws three cards from the deck without looking at them.
On the count of three, each player tosses their cards into the air.

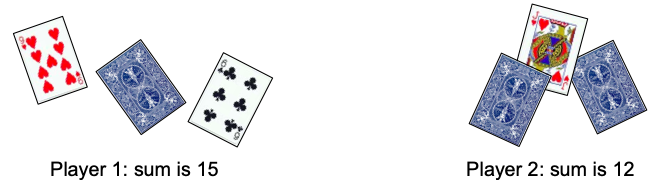
Two groups of 3 cards, Player 1 has one card that is face down, and 2 cards face up, 9 of hearts and 6 of clubs. Player 2 has 2 cards that are face down and 1 card face up a Jack of hearts.

Points are earned for every card that lands face up.
An Ace is worth 11, a Jack is worth 12, a Queen is worth 13 and a King is worth 14.
Each player adds only their own cards that land face up.
Players record their score on a piece of paper and keep a running total.

The first player to reach a designated amount of points wins (50 or 100).

Possible Adaptation:

Remove the face cards and Aces.

Adapted from Acing Math.

Triangle Block

Materials:

  • Technology to access the internet (e.g., smartphone, tablet, laptop, Chromebook, computer etc.)

This is a game for two people using this virtual game board.

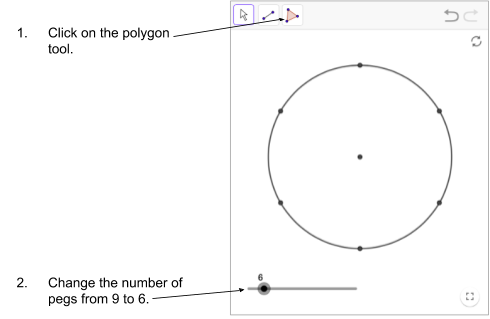
A screen capture of the virtual game board containing a circle with 6 pegs equally spaced on the outline of the circle and 1 peg in the center of the circle.

How to play:

Players take turns adding a band to the board by clicking on the pegs they want the band to go around.

Bands must fit around three pegs to make a triangle.

A band can share a peg with other bands and your triangle can share the side of another triangle but the triangles can’t overlap.

A player loses when they cannot make a triangle on their turn.

What triangle could you make first?
What could you do next?
Could you have done something different to start with?
Is it better to go first or second? Why?

Possible Adaptations:

You could start with 4 pegs to introduce the game with fewer possibilities.
You could increase the number of pegs to provide more possibilities.
You could allow for other shapes like quadrilaterals.

Adapted from nrich.maths.org

The Path to 100

Materials:

  • copies of the maze (or if you don’t have access to a printer you could make your own copies)
  • pencil
  • paper

In this maze there are numbers in each of the “cells”. As you go through you need to add all the numbers that you pass. You may not go through any “cell” more than once.

Can you find a way through in which the numbers add to exactly 100?

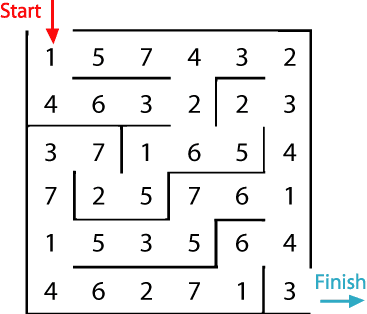
A maze containing a variety of numbers from 1 to 7.

What is the lowest number you can make going through the maze?
What is the highest number you can make going through the maze? (Remember you may not go through any cell more than once.)

Possible Questions/Hints

How are you choosing where to go next?
How are you keeping track of the numbers you need to add?
How could you change your path to get closer to 100 rather than starting again at the beginning?
How could you keep track of the paths you have tried?

Adapted from nrich.maths.org