Problem Solving Prompts

Learning Goals:

  • Develop an understanding of simple multiplicative relationships involving rates
  • Communicate mathematical thinking orally and visually

The Challenge:

Aarav loves walking the 2 km loop around the local park with his Mom, sister, and brother.
They usually split up into two groups – Aarav walks with his sister, while his younger brother walks the loop with his Mom.
Aarav and his sister walk at a pace of 6 km/h, while his Mom and younger brother walk at a slower pace of 4 km/h.

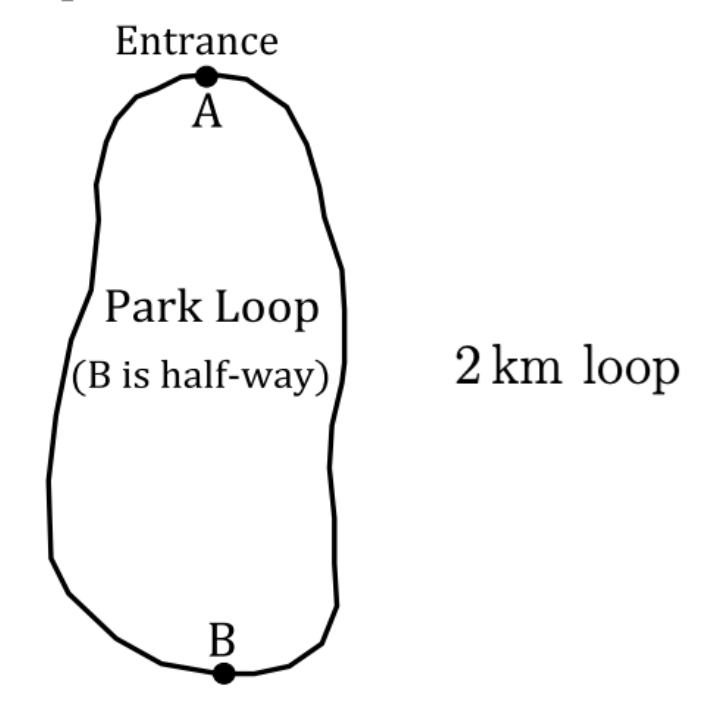
An image of an oval-shaped walking loop labelled 2km long. Point A at the top of the loop is labelled as the entrance, with point B at the bottom of the loop marked as the half-way point.

If everyone starts at the entrance together, walking in the same direction, where will Aarav and his sister be after ½ hour of walking together? Where will Aarav’s Mom and younger brother be?
If they all walk for 2 ½ hours, how many times will Aarav and his sister pass by his Mom and younger brother?
How many laps will each pair complete? Where will each pair end up at the end of this time?

Questions and Prompts to Support your Child:

  • What have you tried? If that didn’t work, try tracing your way around the loop as you count up the distance travelled!
  • If you’re not sure how to get started, remember that you can use the distance someone would walk in one hour (km/h) to figure out how far someone would walk in ½ hour – they would walk half as far!

Extensions & Adaptations:

  • If you were planning a walk so that both groups would finish in the same spot, how long of a walk would you plan? What if you wanted both groups to finish specifically at the entrance to the park?
  • When figuring out how many times the two groups would pass each other in 2 ½ hours, how would your solution change if they were walking in opposite directions around the loop?

Source: University of Waterloo – CEMC Problem of the Week Database