Explorations and Games

Learning Goals:

  • Construct triangles using a variety of tools
  • Create and analyse symmetrical designs by translating, reflecting, or rotating a shape

The Challenge:

Creating a Sierpinski Triangle is simple, but results in a beautiful, symmetrical work of art!

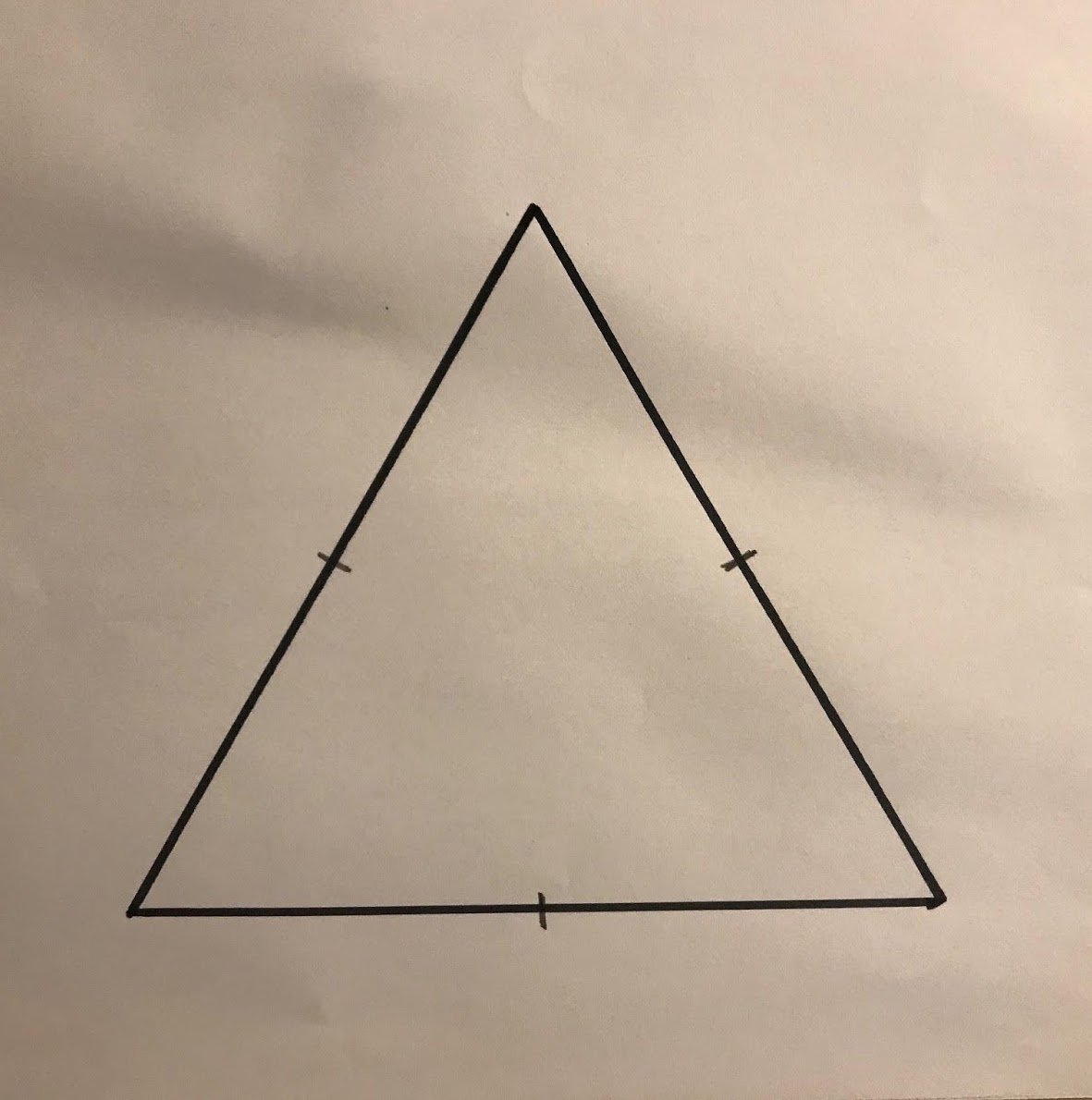
1. Start by creating a large triangle – either on paper or digitally in Mathies Notepad (dot paper option):
(it can be any type of triangle, but most people prefer equilateral)

Outline sketch of an equilateral triangle.

2. Mark the middle of each side of your triangle with a dot or tick mark:
(You can measure this or estimate – it’s up to you!)

Outline sketch of an equilateral triangle with tick marks indicating the midpoint of each side.

3. Connect those midpoint marks with straight lines:

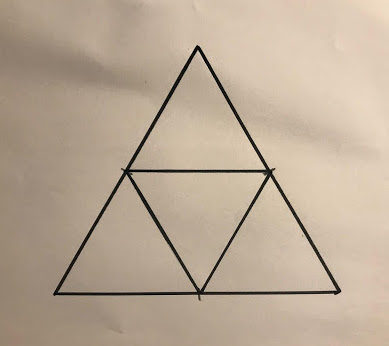
An equilateral triangle with three internal lines connecting at the midpoints.

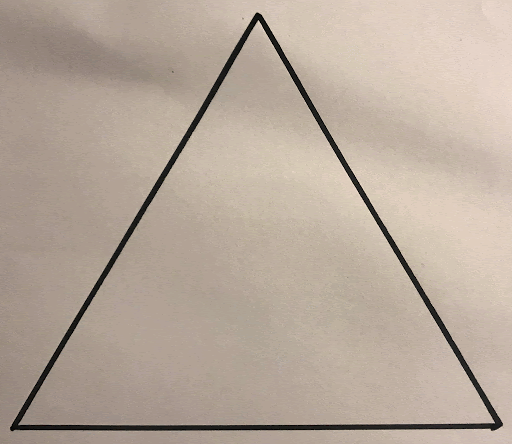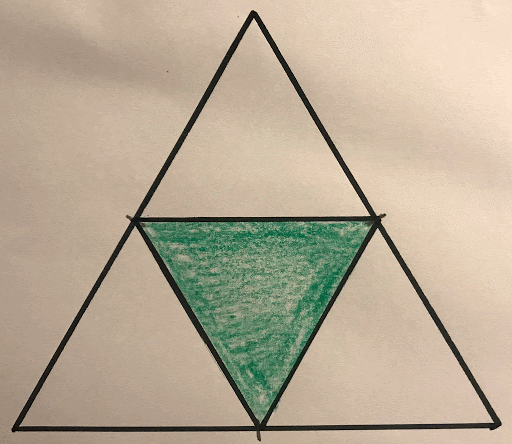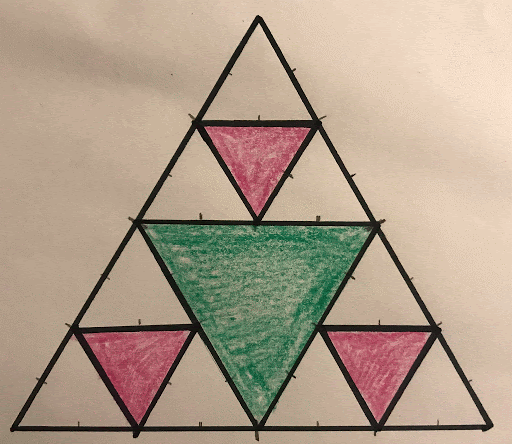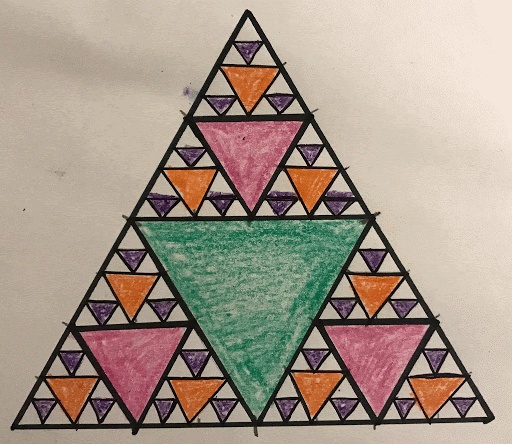
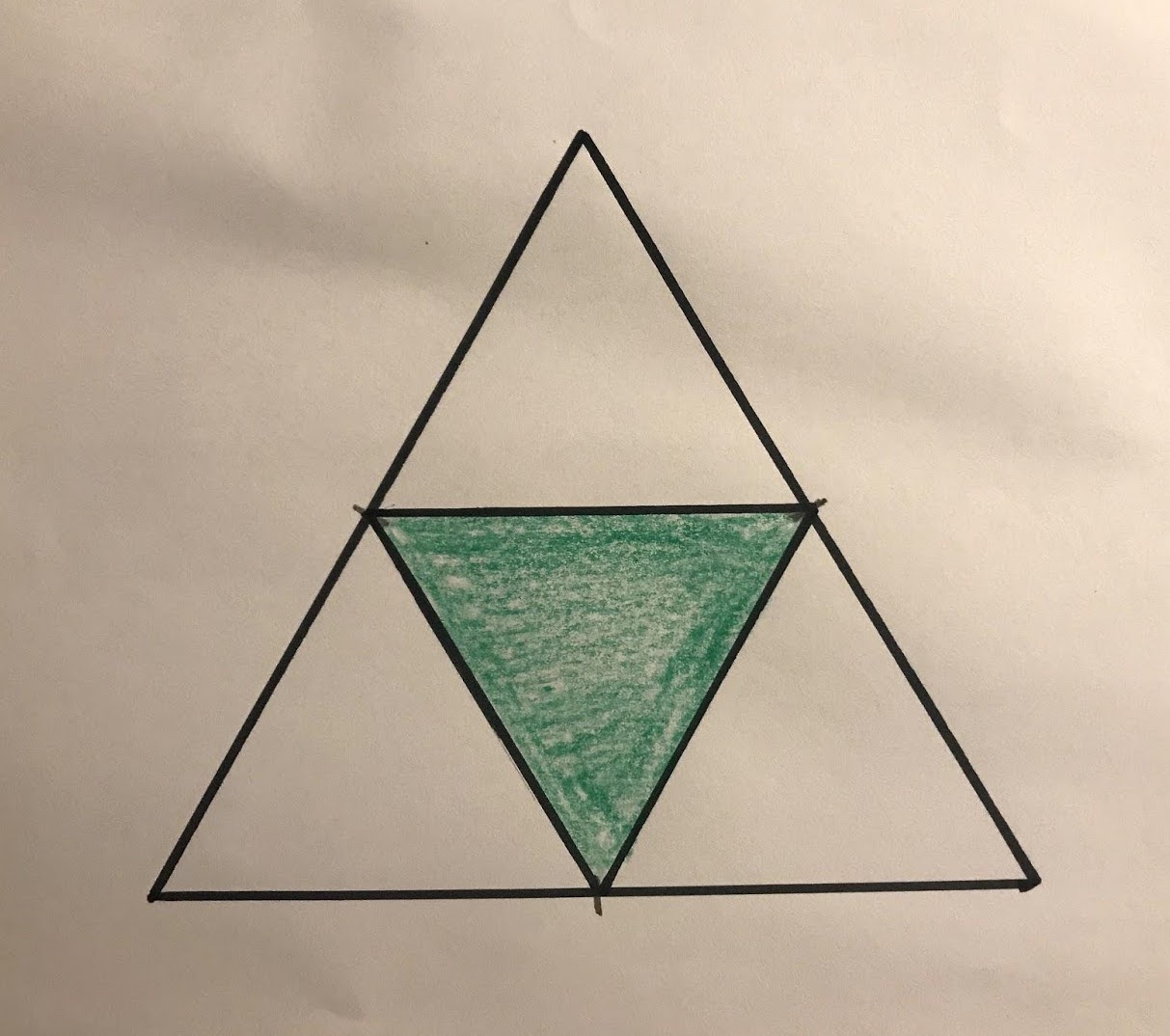
4. Now you should see that your original triangle is now made up of 4 similar triangles, 3 facing the same direction of the original, and 1 that is upside down.

Colour in (or shade) the upside-down triangle:

An equilateral triangle with a smaller, downward pointing green triangle contained inside.

Next, follow steps 2, 3, and 4 for your new smaller blank triangles, except choose a new colour for these new upside down triangles. You should end up with something like this:

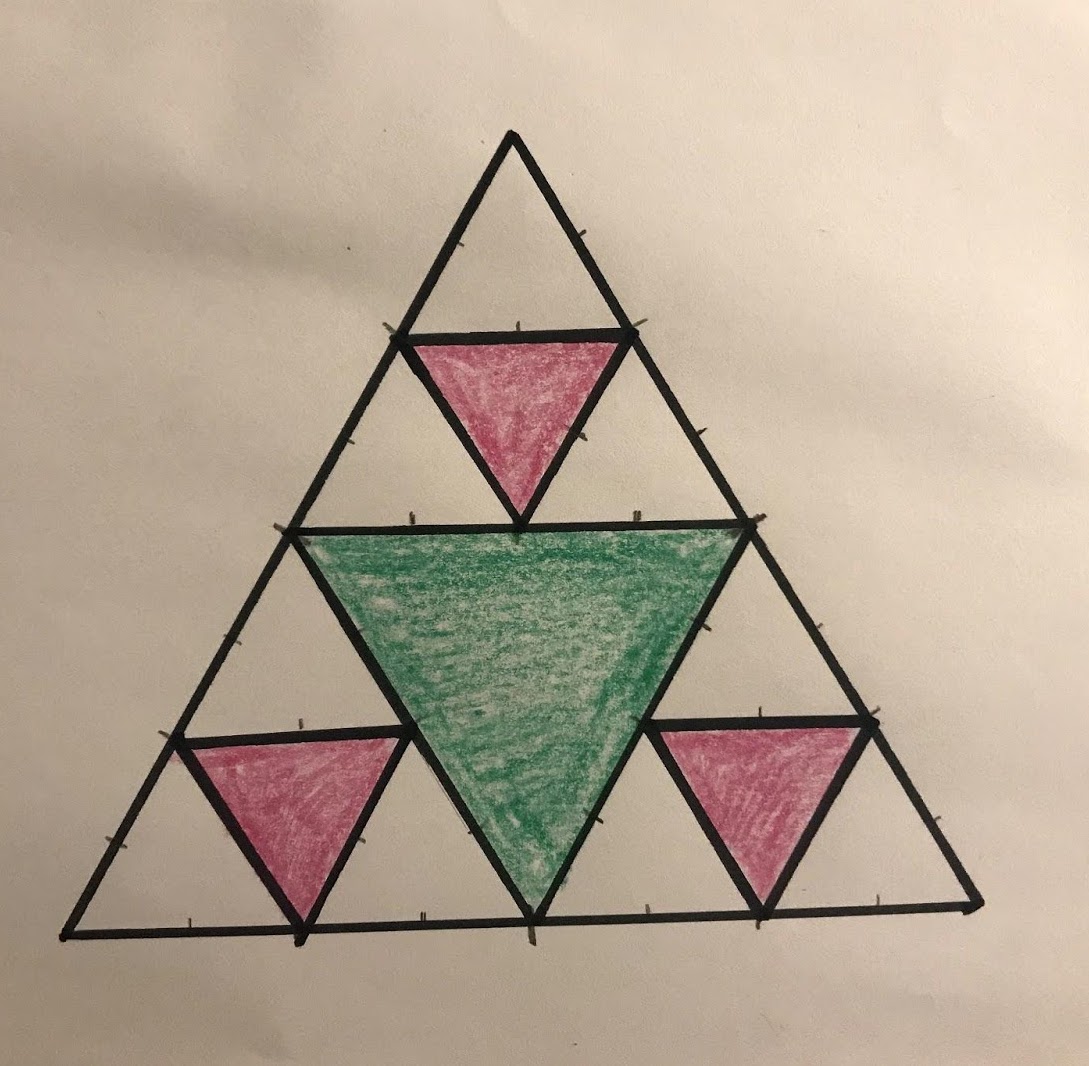
An equilateral triangle with a green triangle in the centre, surrounded by smaller, pink triangles.
Now each corner section matches what you created in step four! (a triangle divided into 4 smaller triangles) That’s what is interesting about the Sierpinski triangle – every section looks like a miniature version of the whole thing. It’s what’s known as a fractal in Mathematics.

How many more stages can you go from here?
The larger your starting triangle, the farther you can get, and the more complex your finished work of art will be!

A completed Sierpinski Triangle containing a large green triangle, three medium pink triangles, nine small orange triangles, and twenty-seven tiny purple triangles.

Stage 4

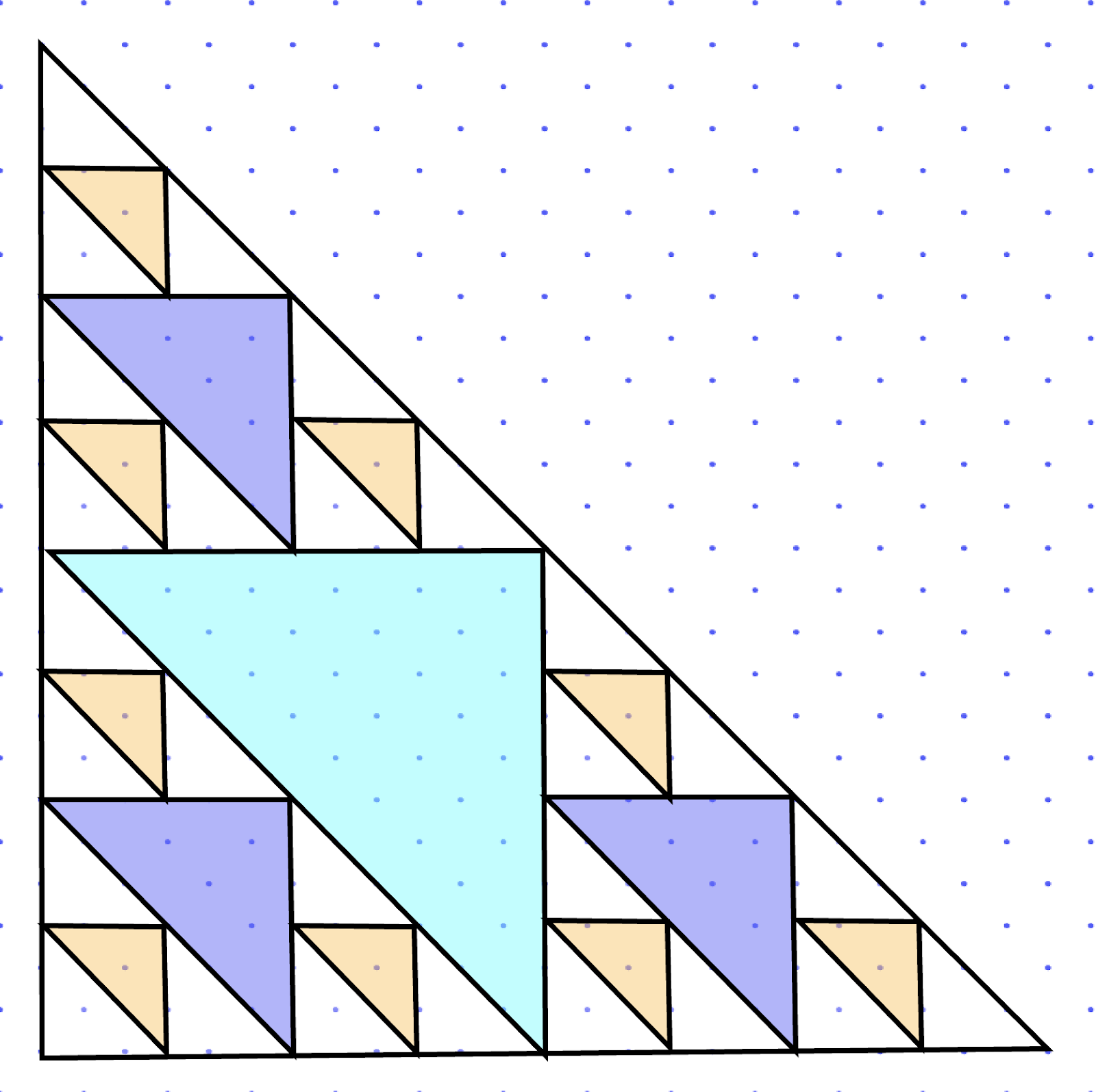
A completed Sierpinski Triangle containing a large teal triangle, three medium blue triangles, and nine small orange triangles.

Stage 3

Extensions, Adaptations, and Math Conversations:

  • What changes when you change your original triangle? (right or isosceles)
  • How many uncolored triangles are there after Stage 1? After Stage 2? Stage 3? How is this pattern growing? Can you make predictions about future stages?
  • Check out Mathigon’s Introduction to Fractals if you want to learn more!

Source: Kent Haines – Games for Young Minds