Three identically sized squares, two of which are overlapping.

Investigations

Materials:

paper, pencil
3 square frames (made from paper or straws and tape, or use the virtual version here.)

Getting Started:

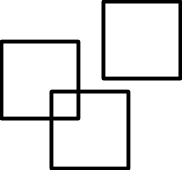
Start with 2 squares:
What is the greatest number of squares you can make by overlapping 2 squares?
Experiment by overlapping them in different ways. Ask your child to count the number of squares they see. (the original big squares count).
You might have a debate about which ones are squares and how you can tell.

They can trace or copy the squares on paper and colour the different squares or label them with numbers to keep track of the arrangement with the most squares.

Possible Questions:

How many squares can you make by overlapping two large squares?
How do you know when a shape is a square?
Can you move the large squares so that you create more squares?
How do you know that it isn’t possible to make more squares?

Next Step:

Now try it with 3 squares.
What is the greatest number of squares you can make by overlapping 3 squares?

(Hint: there are more than 5)

Extension:

Try it with 4 squares or 3 equilateral triangles.

Adapted from nrichmaths.org